
- Read more about Rumour Source Detection in Social Networks using Partial Observations
- Log in to post comments
- Categories:
 22 Views
22 Views
- Read more about Convolutional Neural Networks via Node-Varying Graph Filters
- Log in to post comments
Convolutional neural networks (CNNs) are being applied to an increasing number of problems and fields due to their superior performance in classification and regression tasks. Since two of the key operations that CNNs implement are convolution and pooling, this type of networks is implicitly designed to act on data described by regular structures such as images. Motivated by the recent interest in processing signals defined in irregular domains, we advocate a CNN architecture that operates on signals supported on graphs.
- Categories:
 42 Views
42 Views
In this work, we jointly exploit tools from graph signal processing and control theory to drive a bandlimited graph signal that is being diffused on a random time-varying graph from a subset of nodes. As our main contribution, we rely only on the statistics of the graph to introduce the concept of controllability in the mean, and therefore drive the signal on the expected graph to a desired state.
- Categories:
 41 Views
41 Views
We extend the classical joint problem of signal demixing, blind deconvolution,
and filter identification to the realm of graphs. The model is that
each mixing signal is generated by a sparse input diffused via a graph filter.
Then, the sum of diffused signals is observed. We identify and address
two problems: 1) each sparse input is diffused in a different graph; and 2)
all signals are diffused in the same graph. These tasks amount to finding
the collections of sources and filter coefficients producing the observation.
- Categories:
 36 Views
36 Views
The ability to obtain accurate estimators from a set of measurements is a key factor in science and engineering. Typically, there is an inherent assumption that the measurements were taken in a sequential order, be it in space or time. However, data is increasingly irregular so this assumption of sequentially obtained measurements no longer holds. By leveraging notions of graph signal processing to account for these irregular domains, we propose an unbiased estimator for the mean of a wide sense stationary graph process based on the diffusion of a single realization.
- Categories:
 99 Views
99 Views
- Read more about Tracking Time-Vertex Propagation using Dynamic Graph Wavelets
- Log in to post comments
Graph Signal Processing generalizes classical signal processing to signal or data indexed by the vertices of a weighted graph. So far, the research efforts have been focused on static graph signals. However numerous applications involve graph signals evolving in time, such as spreading or propagation of waves on a network. The analysis of this type of data requires a new set of methods that takes into account the time and graph dimensions. We propose a novel class of wavelet frames named Dynamic Graph Wavelets, whose time-vertex evolution follows a dynamic process.
- Categories:
 10 Views
10 Views
- Read more about Rethinking Sketching as Sampling: Efficient Approximate Solution to Linear Inverse Problems
- Log in to post comments
Sampling and reconstruction of bandlimited graph signals have well-appreciated merits for dimensionality reduction, affordable storage, and online processing of streaming network data. However, these parsimonious signals are oftentimes encountered with high-dimensional linear inverse problems. Hence, interest shifts from reconstructing the signal itself towards instead approximating the input to a prescribed linear operator efficiently.
- Categories:
 8 Views
8 Views
- Read more about Rethinking Sketching as Sampling: Efficient Approximate Solution to Linear Inverse Problems
- Log in to post comments
Sampling and reconstruction of bandlimited graph signals have well-appreciated merits for dimensionality reduction, affordable storage, and online processing of streaming network data. However, these parsimonious signals are oftentimes encountered with high-dimensional linear inverse problems. Hence, interest shifts from reconstructing the signal itself towards instead approximating the input to a prescribed linear operator efficiently.
- Categories:
 13 Views
13 Views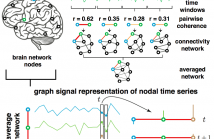
- Read more about Graph Frequency Analysis of Brain Signals
- Log in to post comments
This paper presents methods to analyze functional brain networks and signals from graph spectral perspectives. The notion of frequency and filters traditionally defined for signals supported on regular domains such as discrete time and image grids has been recently generalized to irregular graph domains, and defines brain graph frequencies associated with different levels of spatial smoothness across the brain regions. Brain network frequency also enables the decomposition of brain signals into pieces corresponding to smooth or rapid variations.
- Categories:
 131 Views
131 Views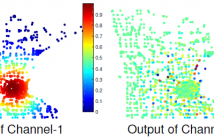
- Read more about Graph Filter Banks With M-Channels, Maximal Decimation, and Perfect Reconstruction
- Log in to post comments
Signal processing on graphs finds applications in many areas. Motivated by recent developments, this paper studies the concept of spectrum folding (aliasing) for graph signals under the downsample-then-upsample operation. In this development, we use a special eigenvector structure that is unique to the adjacency matrix of M-block cyclic matrices. We then introduce M-channel maximally decimated filter banks. Manipulating the characteristics of the aliasing effect, we construct polynomial filter banks with perfect reconstruction property.
- Categories:
 44 Views
44 Views