Sorry, you need to enable JavaScript to visit this website.

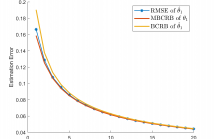
Point processes are finding increasing applications in neuroscience, genomics, and social media. But basic modelling properties are little studied. Here we consider a periodic time-varying Poisson model and develop the asymptotic Cramer-Rao bound. We also develop, for the first time, a maximum likelihood algorithm for parameter estimation.

Consider the set of possible observations turned out by geometric and radiometric transformations of an object. This set is generally a manifold in the ambient space of observations. It has been shown [1] that in those cases where the geometric deformations are affine and the radiometric deformations are monotonic, the radiometry invariant universal manifold embedding (RIUME) provides a mapping from the orbit of deformed observations to a single low dimensional linear subspace of Euclidean space.

Variational nonlinear chirp mode decomposition (VNCMD) is a recently introduced method for nonlinear chirp signal decomposition that has aroused notable attention in various fields. One limiting aspect of the method is that its performance relies heavily on the setting of the bandwidth parameter.

Bioimpedance is a powerful modality to continuously and non-invasively monitor cardiovascular and respiratory health parameters through the wearable operation. However, for bioimpedance sensors to be utilized in medical-grade settings, the reliability and robustness of the system should be improved. Previous studies provide limited fundamental analyses of the factors involved in the system that impact the sensitivity and the specificity of the modality in capturing the hemodynamics.

Graphs are fundamental mathematical structures used in various fields to model statistical and physical relationships between data, signals, and processes. In some applications, such as data processing in graphs that represent physical networks, the initial network topology is known. However, disconnections of edges in the network change the topology and may affect the signals and processes over the network. In this paper, we consider the problem of edge disconnection identification in networks by using concepts from graph signal processing.

Many activities such as drilling and exploration in the oil and gas industries rely on identifying seismic faults. Using graph high-frequency components as inputs to a graph convolutional network, we propose a method for detecting faults in seismic data. In Graph Signal Processing (GSP), digital signal processing (DSP) concepts are mapped to define the processing techniques for signals on graphs. As a first step, we extract patches of the seismic data centered around the points of concern. Each patch is then represented in a graph domain, with the seismic amplitudes as the graph signals.

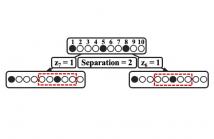
This paper studies the problem of discrete super-resolution. Existing stability guarantees rely on the fact that certain sep- aration conditions are satisfied by the true support. However, such structural conditions have not been exploited in the cor- responding algorithmic designs. This paper proposes a novel Bayesian approach based on the model aggregation idea that can generate an exact sparse estimate, and maintain the re- quired structures of the support.