
- Read more about 3DLaneFormer: Rethinking Learning Views for 3D Lane Detection
- Log in to post comments
Accurate 3D lane detection from monocular images is crucial for autonomous driving. Recent advances leverage either front-view (FV) or bird’s-eye-view (BEV) features for prediction, inevitably limiting their ability to perceive driving environments precisely and resulting in suboptimal performance. To overcome the limitations of using features from a single view, we design a novel dual-view cross-attention mechanism, which leverages features from FV and BEV simultaneously. Based on this mechanism, we propose 3DLaneFormer, a powerful framework for 3D lane detection.
- Categories:
 90 Views
90 Views
- Read more about SynTable: A Synthetic Data Generation Pipeline for Unseen Object Amodal Instance Segmentation of Cluttered Tabletop Scenes (Supplementary Materials)
- Log in to post comments
In this work, we present SynTable, a Python-based dataset generator built using NVIDIA's Isaac Sim Replicator Composer for generating high-quality synthetic datasets for unseen object amodal instance segmentation of cluttered tabletop scenes. Our tool renders complex 3D scenes containing object meshes, materials, textures, lighting, and backgrounds. Metadata, including modal and amodal instance segmentation masks, occlusion masks, depth maps, and bounding boxes can be automatically generated based on user requirements.
- Categories:
 26 Views
26 Views
We address distinguishing whether an input is a facial image by learning only a facial-expression recognition (FER) dataset.
- Categories:
 64 Views
64 Views
We address distinguishing whether an input is a facial image by learning only a facial-expression recognition (FER) dataset.
- Categories:
 29 Views
29 Views
- Read more about Pairwise Feature Learning for Unseen Plant Disease Recognition
- Log in to post comments
With the advent of Deep Learning, people have begun to use it with computer vision approaches to identify plant diseases on a large scale targeting multiple crops and diseases. However, this requires a large amount of plant disease data, which is often not readily available, and the cost of acquiring disease images is high. Thus, developing a generalized model for recognizing unseen classes is very important and remains a major challenge to date. Existing methods solve the problem with general supervised recognition tasks based on the seen composition of the crop and the disease.
- Categories:
 39 Views
39 Views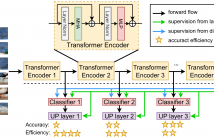
- Read more about MULTI-EXIT VISION TRANSFORMER WITH CUSTOM FINE-TUNING FOR FINE-GRAINED IMAGE RECOGNITION
- Log in to post comments
Capturing subtle visual differences between subordinate categories is crucial for improving the performance of Finegrained Visual Classification (FGVC). Recent works proposed deep learning models based on Vision Transformer (ViT) to take advantage of its self-attention mechanism to locate important regions of the objects and extract global information. However, their large number of layers with self-attention mechanism requires intensive computational cost and makes them impractical to be deployed on resource-restricted hardware including internet of things (IoT) devices.
- Categories:
 62 Views
62 Views
- Read more about UTILIZING SUPER-RESOLUTION FOR ENHANCED AUTOMOTIVE RADAR OBJECT DETECTION
- Log in to post comments
In recent years, automotive radar has become an integral part of the advanced safety sensor stack. Although radar gives a significant advantage over a camera or Lidar, it suffers from poor angular resolution, unwanted noises and significant object smearing across the angular bins, making radar-based object detection challenging. We propose a novel radar-based object detection utilizing a deep learning-based super-resolution (DLSR) model. Due to the unavailability of low-high resolution radar data pair, we first simulate the data to train a DLSR model.
- Categories:
 45 Views
45 Views
- Read more about A Multichannel Localization Method for Camouflaged Object Detection
- Log in to post comments
This paper proposes a multichannel method for discriminative region localization in Camouflaged Object Detection (COD) tasks. In one channel, processing the phase and amplitude of 2-D Fourier spectra generate a modified form of the original image, used later for a pixel-wise optimal local entropy analysis. The other channel implements a class activation map (CAM) and Global Average Pooling (GAP) for object localization. We combine the channels linearly to form the final localized version of the COD images.
- Categories:
 102 Views
102 Views
- Read more about A Multichannel Localization Method for Camouflaged Object Detection
- Log in to post comments
This paper proposes a multichannel method for discriminative region localization in Camouflaged Object Detection (COD) tasks. In one channel, processing the phase and amplitude of 2-D Fourier spectra generate a modified form of the original image, used later for a pixel-wise optimal local entropy analysis. The other channel implements a class activation map (CAM) and Global Average Pooling (GAP) for object localization. We combine the channels linearly to form the final localized version of the COD images.
- Categories:
 18 Views
18 Views- Read more about Functional Knowledge Transfer with Self-supervised Representation Learning
- Log in to post comments
This work investigates the unexplored usability of self-supervised representation learning in the direction of functional knowledge transfer. In this work, functional knowledge transfer is achieved by joint optimization of self-supervised learning pseudo task and supervised learning task, improving supervised learning task performance. Recent progress in self-supervised learning uses a large volume of data, which becomes a constraint for its applications on small-scale datasets.
- Categories:
 48 Views
48 Views