- Signal and System Modeling, Representation and Estimation
- Multirate Signal Processing
- Sampling and Reconstruction
- Nonlinear Systems and Signal Processing
- Filter Design
- Adaptive Signal Processing
- Statistical Signal Processing

We introduce the Generative Barankin Bound (GBB), a learned Barankin Bound, for evaluating the achievable performance in estimating the direction of arrival (DOA) of a source in non-asymptotic conditions, when the statistics of the measurement are unknown. We first learn the measurement distribution using a conditional normalizing flow (CNF) and then use it to derive the GBB.
- Categories:
 31 Views
31 Views
- Read more about A SALIENCY ENHANCED FEATURE FUSION BASED MULTISCALE RGB-D SALIENT OBJECT DETECTION NETWORK
- 1 comment
- Log in to post comments
Multiscale convolutional neural network (CNN) has demonstrated remarkable capabilities in solving various vision problems. However, fusing features of different scales always results in large model sizes, impeding the application of mul-
tiscale CNNs in RGB-D saliency detection. In this paper, we propose a customized feature fusion module, called Saliency Enhanced Feature Fusion (SEFF), for RGB-D saliency detection. SEFF utilizes saliency maps of the neighboring scales
- Categories:
 26 Views
26 Views
- Read more about Poster of the paper "Multivariate Density Estimation Using Low-Rank Fejér-Riesz Factorization"
- Log in to post comments
We consider the problem of learning smooth multivariate probability density functions. We invoke the canonical decomposition of multivariate functions and we show that if a joint probability density function admits a truncated Fourier series representation, then the classical univariate Fejér-Riesz Representation Theorem can be used for learning bona fide joint probability density functions. We propose a scalable, flexible, and direct framework for learning smooth multivariate probability density functions even from potentially incomplete datasets.
- Categories:
 52 Views
52 Views
- Read more about Restoration of Time-Varying Graph Signals using Deep Algorithm Unrolling
- Log in to post comments
In this paper, we propose a restoration method of time-varying graph signals, i.e., signals on a graph whose signal values change over time, using deep algorithm unrolling. Deep algorithm unrolling is a method that learns parameters in an iterative optimization algorithm with deep learning techniques. It is expected to improve convergence speed and accuracy while the iterative steps are still interpretable. In the proposed method, the minimization problem is formulated so that the time-varying graph signal is smooth both in time and spatial domains.
- Categories:
 74 Views
74 Views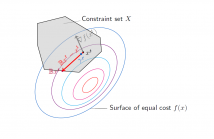
- Read more about EUSIPCO 2017 Tutorial: Exploiting structure and pseudo-convexity in iterative parallel optimization algorithms for real-time and large scale applications
- Log in to post comments
In the past two decades convex optimization gained increasing popularity in signal processing and communications, as many fundamental problems in this area can be modelled, analyzed and solved using convex optimization theory and algorithms. In emerging large scale applications such as compressed sensing, massive MIMO and machine learning, the underlying optimization problems often exhibit convexity, however, the classic interior point methods do not scale well with the problem dimensions.
- Categories:
 100 Views
100 Views
The unlabeled sensing problem is to solve a noisy linear system of equations under unknown permutation of the measurements. We study a particular case of the problem where the
- Categories:
 20 Views
20 Views
- Read more about Proximal-based adaptive simulated annealing for global optimization (slides)
- Log in to post comments
Simulated annealing (SA) is a widely used approach to solve global optimization problems in signal processing. The initial non-convex problem is recast as the exploration of a sequence of Boltzmann probability distributions, which are increasingly harder to sample from. They are parametrized by a temperature that is iteratively decreased, following the so-called cooling schedule. Convergence results of SA methods usually require the cooling schedule to be set a priori with slow decay. In this work, we introduce a new SA approach that selects the cooling schedule on the fly.
- Categories:
 15 Views
15 Views
- Read more about Proximal-based adaptive simulated annealing for global optimization (poster)
- Log in to post comments
Simulated annealing (SA) is a widely used approach to solve global optimization problems in signal processing. The initial non-convex problem is recast as the exploration of a sequence of Boltzmann probability distributions, which are increasingly harder to sample from. They are parametrized by a temperature that is iteratively decreased, following the so-called cooling schedule. Convergence results of SA methods usually require the cooling schedule to be set a priori with slow decay. In this work, we introduce a new SA approach that selects the cooling schedule on the fly.
- Categories:
 14 Views
14 Views
- Read more about Learning Expanding Graphs for Signal Interpolation
- Log in to post comments
- Categories:
 9 Views
9 Views
- Read more about Learning Expanding Graphs for Signal Interpolation
- Log in to post comments
- Categories:
 24 Views
24 Views