- Signal and System Modeling, Representation and Estimation
- Multirate Signal Processing
- Sampling and Reconstruction
- Nonlinear Systems and Signal Processing
- Filter Design
- Adaptive Signal Processing
- Statistical Signal Processing

Many information sources are not just sequences of distinguishable symbols but rather have invariances governed by alternative counting paradigms such as permutations, combinations, and partitions. We consider an entire classification of these invariances called the twelvefold way in enumerative combinatorics and develop a method to characterize lossless compression limits. Explicit computations for all twelve settings are carried out for i.i.d. uniform and Bernoulli distributions. Comparisons among settings provide quantitative insight.
- Categories:
 58 Views
58 Views
- Read more about UNSUPERVISED AUTO-ENCODING MULTIPLE-OBJECT TRACKER FOR CONSTRAINT-CONSISTENT COMBINATORIAL PROBLEM
- Log in to post comments
Multiple-object tracking (MOT) and classification are core technologies for processing moving point clouds in radar or lidar applications. For accurate object classification, the one-to-one association relationship between the model of each objects' motion (trackers) and the observation sequences including auxiliary features (e.g., radar cross section) is important.
- Categories:
 67 Views
67 Views
- Read more about UNSUPERVISED AUTO-ENCODING MULTIPLE-OBJECT TRACKER FOR CONSTRAINT-CONSISTENT COMBINATORIAL PROBLEM
- Log in to post comments
Multiple-object tracking (MOT) and classification are core technologies for processing moving point clouds in radar or lidar applications. For accurate object classification, the one-to-one association relationship between the model of each objects' motion (trackers) and the observation sequences including auxiliary features (e.g., radar cross section) is important.
- Categories:
 46 Views
46 Views
- Categories:
 35 Views
35 Views
- Read more about Recovery of binary sparse signals from compressed linear measurements via polynomial optimization
- 1 comment
- Log in to post comments
- Categories:
 26 Views
26 Views
- Read more about PORTFOLIO CUTS: A GRAPH-THEORETIC FRAMEWORK TO DIVERSIFICATION
- Log in to post comments
- Categories:
 23 Views
23 Views
- Read more about Adaptive prediction of financial time-series for decision-making using a tensorial aggregation approach
- Log in to post comments
Economic and financial decision-making may cause a significant impact on government, society, and industries. Due to the increasing volume of data, decision science has become an interdisciplinary field of study, supported by efficient methods and models of data analysis. Our contributions lie exactly in the intersection of signal processing, tensorial algebra, and decision science. More precisely, we introduce a novel approach in which the data taken into account in the decision process is modeled as a tensor.
- Categories:
 24 Views
24 Views
- Read more about β-NMF and sparsity promoting regularizations for complex mixture unmixing: Application to 2D HSQC NMR
- Log in to post comments
In Nuclear Magnetic Resonance (NMR) spectroscopy, an efficient analysis and a relevant extraction of different molecule properties from a given chemical mixture are important tasks, especially when processing bidimensional NMR data. To that end, using a blind source separation approach based on a variational formulation seems to be a good strategy. However, the poor resolution of NMR spectra and their large dimension require a new and modern blind source separation method.
- Categories:
 30 Views
30 Views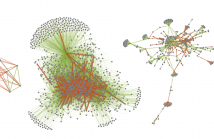
- Read more about LEARNING SIGNED GRAPHS FROM DATA
- Log in to post comments
Signed graphs have recently been found to offer advantages over unsigned graphs in a variety of tasks. However, the problem of learning graph topologies has only been considered for the unsigned case. In this paper, we propose a conceptually simple and flexible approach to signed graph learning via signed smoothness metrics. Learning the graph amounts to solving a convex optimization problem, which we show can be reduced to an efficiently solvable quadratic problem. Applications to signal reconstruction and clustering corroborate the effectiveness of the proposed method.
- Categories:
 77 Views
77 Views
- Read more about Diagonalizable Shift and Filters for Directed Graphs Based on the Jordan-Chevalley Decomposition
- Log in to post comments
Graph signal processing on directed graphs poses theoretical challenges since an eigendecomposition of filters is in general not available. Instead, Fourier analysis requires a Jordan decomposition and the frequency response is given by the Jordan normal form, whose computation is numerically unstable for large sizes. In this paper, we propose to replace a given adjacency shift A by a diagonalizable shift A D obtained via the Jordan-Chevalley decomposition.
- Categories:
 39 Views
39 Views