- Signal and System Modeling, Representation and Estimation
- Multirate Signal Processing
- Sampling and Reconstruction
- Nonlinear Systems and Signal Processing
- Filter Design
- Adaptive Signal Processing
- Statistical Signal Processing

- Read more about [Poster] A Global Cayley Parametrization of Stiefel Manifold for Direct Utilization of Optimization Mechanisms Over Vector Spaces
- Log in to post comments
Optimization problem with orthogonality constraints, whose feasible region is called the Stiefel manifold, has rich applications in data sciences. The severe non-linearity of the Stiefel manifold has hindered the utilization of optimization mechanisms developed specially over a vector space for the problem. In this paper, we present a global parametrization of the Stiefel manifold entirely by a single fixed vector space with the Cayley transform, say Global Cayley Parametrization (G-CP), to solve the problem through optimization over a vector space.
- Categories:
 32 Views
32 Views
- Read more about [Poster] A Variable Smoothing for Nonconvexly Constrained Nonsmooth Optimization with Application to Sparse Spectral Clustering
- Log in to post comments
We propose a variable smoothing algorithm for solving nonconvexly constrained nonsmooth optimization problems. The target problem has two issues that need to be addressed: (i) the nonconvex constraint and (ii) the nonsmooth term. To handle the nonconvex constraint, we translate the target problem into an unconstrained problem by parameterizing the nonconvex constraint in terms of a Euclidean space. We show that under a certain condition, these problems are equivalent in view of finding a stationary point.
- Categories:
 60 Views
60 Views
- Read more about Covariance Matrix Recovery From One-Bit Data With Non-Zero Quantization Thresholds: Algorithm and Performance Analysis
- Log in to post comments
Covariance matrix recovery is a topic of great significance in the field of one-bit signal processing and has numerous practical applications. Despite its importance, the conventional arcsine law with zero threshold is incapable of recovering the diagonal elements of the covariance matrix. To address this limitation, recent studies have proposed the use of non-zero clipping thresholds. However, the relationship between the estimation error and the sampling threshold is not yet known.
- Categories:
 27 Views
27 Views
- Read more about Learning Graphs and Simplicial Complexes from Data
- Log in to post comments
Graphs are widely used to represent complex information and signal domains with irregular support. Typically, the underlying graph topology is unknown and must be estimated from the available data. Common approaches assume pairwise node interactions and infer the graph topology based on this premise. In contrast, our novel method not only unveils the graph topology but also identifies three-node interactions, referred to in the literature as second-order simplicial complexes (SCs).
- Categories:
 36 Views
36 Views
- Read more about LEARNED ISTA WITH ERROR-BASED THRESHOLDING FOR ADAPTIVE SPARSE CODING
- Log in to post comments
Drawing on theoretical insights, we advocate an error-based thresholding (EBT) mechanism for learned ISTA (LISTA), which utilizes a function of the layer-wise reconstruction error to suggest a specific threshold for each observation in the shrinkage function of each layer. We show that the proposed EBT mechanism well disentangles the learnable parameters in the shrinkage functions from the reconstruction errors, endowing the obtained models with improved adaptivity to possible data variations.
poster.pdf
- Categories:
 32 Views
32 Views
- Read more about Computing an Entire Solution Path of a Nonconvexly Regularized Convex Sparse Model
- Log in to post comments
The generalized minimax concave (GMC) penalty is a nonconvex sparse regularizer which can preserve the overall-convexity of the sparse least squares problem. In this paper, we study the solution path of a special but important instance of the GMC model termed the scaled GMC (sGMC) model. We show that despite the nonconvexity of the regularizer, there exists a solution path of the sGMC model which is piecewise linear as a function of the regularization parameter, and we propose an efficient algorithm for computing a solution path of this type.
- Categories:
 41 Views
41 Views
- Read more about CROSS BRANCH FEATURE FUSION DECODER FOR CONSISTENCY REGULARIZATION-BASED SEMI-SUPERVISED CHANGE DETECTION
- Log in to post comments
Semi-supervised change detection (SSCD) utilizes partially labeled data and a large amount of unlabeled data to detect changes. However, the transformer-based SSCD network does not perform as well as the convolution-based SSCD network due to the lack of labeled data. To overcome this limitation, we introduce a new decoder called Cross Branch Feature Fusion (CBFF), which combines the strengths of both local convolutional branch and global transformer branch. The convolutional branch is easy to learn and can produce high-quality features with a small amount of labeled data.
- Categories:
 19 Views
19 Views
- Read more about External Division of Two Proximity Operators: An Application to Signal Recovery with Structured Sparsity
- Log in to post comments
This paper studies the external division operator, an external division (an affine combination with positive and negative weights) of two proximity operators. We show that the external division operator is cocoercive under some condition, and it can be expressed as the proximity operator of a certain weakly convex function. We then consider using the external division operator as an alternative to the proximity operator in the proximal gradient algorithm, which we show converges to a minimizer of the cost function penalized by the weakly convex function under some conditions.
- Categories:
 43 Views
43 Views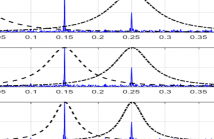
- Read more about Poster for the paper "Dynamic Bandwidth Variational Mode Decomposition"
- Log in to post comments
Signal decomposition techniques aim to break down nonstationary signals into their oscillatory components, serving as a preliminary step in various practical signal processing applications. This has motivated researchers to explore different strategies, yielding several distinct approaches. A wellknown optimization-based method, the Variational Mode Decomposition (VMD), relies on the formulation of an optimization problem utilizing constant-bandwidthWiener filters. However, this poses limitations in constant bandwidth and the need for constituent count.
- Categories:
 29 Views
29 Views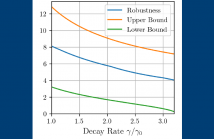
Nuclear magnetic resonance (NMR) spectroscopy is routinely used to study the properties of matter. Therefore, different materials can be classified according to their NMR spectra. However, the NMR spectra cannot be observed directly, and only the NMR signal, which is a sum of complex exponentials, is directly observable in practice. A popular approach to recover the spectrum is to perform harmonic retrieval, i.e., to reconstruct exactly the spectrum from the NMR signal. However, even when this approach fails, the spectrum might still be classified accurately.
- Categories:
 109 Views
109 Views